Nous obtenons ainsi la fonction de Poisson ou loi de Poisson appelée également parfois loi des événements rares donnée donc par. Introduction aux lois de probabilité avec R Christophe Chesneau To cite this version.
Loi de Poisson et Contents Fonction génératrice Nous terminons cette première partie en introduisant la notion de fonction génératrice qui est un outil permettant de simplifier le calcul despérances.
Fonction de répartition loi de poisson. La loi de Poisson est une loi de probabilité discrète qui modélise un nombre dévénements à partir dun taux doccurrence constant. Si λ15 alors cette loi de Poisson Pλ peut être approximée par une loi normale Alors la variable suit une normale centrée réduite N01. F est une fonction positive sur.
Statistiques 4 Année universitaire 2015-2016 Cours de Mme Chevalier Lois de probabilité usuelles rappels Généralités Fonction de répartition dune loi discrète. Approximation de la loi de Poisson par la loi normale. En théorie des probabilités et en statistiques la loi de Poisson est une loi de probabilité discrète qui décrit le comportement du nombre dévénements se produisant dans un intervalle de temps fixé si ces événements se produisent avec une fréquence moyenne ou espérance connue et indépendamment du temps écoulé depuis lévénement précédent.
Pour effectuer un calcul avec une de ces lois il suffit dutiliser comme fonction lune des appellations R ci-dessus avec le préfixe d pour une densité p pour une fonction de. Mohamed El Merouani 13 Exemple. Le resultat suivant est a la base de la methode dinversion de la fonction de repartition qui permet de simuler des variables aleatoires reelles.
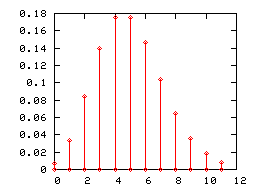
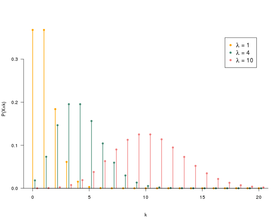
Comme toute loi de probabilité discrète une loi de Poisson peut être représentée par un diagramme en bâtonsCi-dessous sont représentés les diagrammes en bâtons des lois de Poisson de paramètres 1 2 et 5. Cependant pour parer aux aléas dune demande importante soudaine dune demande fluctuante ou dune demande peu fréquente généralement un stock de sécurité est constitué. On appelle X la variable aléatoire déterminant le nombre.
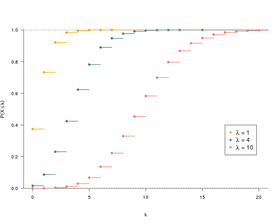
La fonction de répartition sécrit donc. La taille du stock est calculée en utilisant la loi de Poisson. La notion de nombre en linguistique est traitée à larticle Nombre.
Scientifiques de niveau recherche publiés ou non émanant des établissements denseignement et de recherche français ou étrangers des laboratoires publics ou privés. Nλ λ Soit une va. F_X_lambdan PX_lambdaleqslant n sum_0le kleqslant nPX_lambdak e-lambda cdot smashunderbracesum_k0n fraclambdakk_S_nlambda.
Parmi les plus utilisées la loi uniforme unif porte par défaut sur lintervalle et la loi normale norm est centrée réduite par défaut. La loi de Poisson est également pertinente pour décrire le nombre dévénements dans dautres types dintervalles spatiaux. Pour certaines lois les paramètres ont des valeurs par défaut.
Qui suit une loi de Poisson de paramètre λ. Définition et Explications - En théorie des probabilités et en statistiques la loi de Poisson est une loi de probabilité discrète qui décrit le comportement du nombre dévènements se produisant dans un laps de temps fixé si ces évènements se produisent avec une fréquence moyenne connue et indépendamment du temps écoulé depuis lévènement précédent. Moments et variance dune va.
En statistique la loi de Poisson de paramètre λ ou loi des événements rares correspond au modèle suivant. FONCTION DE REPARTITION ET COPULE. Applications Gestion des stocks En demande normale le stock est approvisionné en fonction de la consommation moyenne.
La formule 26421 de Abramowitz et Stegun Handbook of Mathematical Functions 1966 est utilisée pour réduire le calcul de la fonction de répartition de la distribution à celle dune loi gamma incomplète. - La loi de poisson intervient souvent lorsquon compte des événements rares comme les suicides denfants les arrivées de bateaux dans un port ou les accidents dus aux coups de pied de cheval dans les armées étude de ladislaus bortkiewiczle décompte des événements rares se fait souvent au travers dune somme de variables de bernoulli et la rareté des événements se traduit par le. Fonction de répartition dune va.
La fonction LOINORMALEN renvoie la distribution normale. Introduction aux lois de probabilité avec R. En probabilité on appelle fonction de densité de probabilité f toute fonction de dans qui vérifie les conditions suivante.
Ce que vous cherchez - Fonction De Répartition De La Loi De Poisson. Théorème limite de Poisson. La loi de Poisson peut être utilisée comme approximation de la loi binomiale lorsque le nombre dessais indépendants est élevé et que la probabilité de réussite est faible.
Si X i sont distribuées selon des lois Γα i θ respectivement alors le vecteur X 1 S X n S où S X 1. F est continue sur sauf en un nombre fini de points. λ λ X T Prof.
La fonction LOINORMALEN dExcel. Sur une période T un événement arrive en moyenne λ fois. Diagramme en bâton modifier modifier le code.
Cette technique de passage à la limite est parfois appelée dans ce contexte. X n suit une distribution de Dirichlet de paramètres α 1 α n. Lorsque le paramètre λ de la loi de Poisson devient grand pratiquement lorsquil est supérieur à 5 son diagramme en.
Loi dune fonction dune va. Étant donnés les autres calcule un paramètre de la distribution de Poisson. Si X et Y sont distribuées indépendamment selon des lois Γα θ et Γβ θ respectivement alors X X Y a une distribution beta de paramètres α et β.
On définit également la fonction de répartition F définie par. Loi de Poisson P5 Loi uniforme sur 010 Loi gaussienne N01.
Loi De Poisson Wikipedia
Loi De Poisson Wikipedia
Loi De Poisson Wikipedia
Loi De Poisson Wikipedia
Loi De Poisson Homeomath
